Miller Anestesia

984 / 2894

medir el volumen de orina es un ejemplo. El volúmetro usado en
las máquinas de anestesia Drager de Estados Unidos también mide
las alícuotas de volumen integradas en el tiempo para medir el
volumen corriente y por minuto .
Medidores de flujo dilucionales
(termodilución, principio de Fick)
El flujo de la masa y el volumen puede medirse con técnicas de
dilución. Si se inyecta algún indicador mensurable (un bolo
de tinte, un pulso termal, el consumo de oxígeno, la producción de
dióxido de carbono) en un flujo, y su concentración se mide más
adelante en función del tiempo, el flujo de volumen (Q) puede
calcularse por integración. La aplicación médica más frecuente es
la determinación del gasto cardíaco por el método de termodilu-
ción de la arteria pulmonar (v. apéndice 6). Los errores que se
asocian con estos métodos se relacionan con el uso de un volumen
inyectable erróneo (un volumen demasiado pequeño produce un
flujo demasiado grande) o un error de la medida de la temperatura
(v. sección sobre temperatura).
Los sistemas de medición del gasto cardíaco «continuo» que
utilizan una espiral calentada por electricidad para calentar la
sangre de la arteria pulmonar evitan errores asociados con las téc-
nicas de inyectado de líquidos, pero crean la necesidad de calcular
la señal más pequeña a lo largo de un intervalo de tiempo más largo.
Además, hay un límite superior al que se puede calentar la sangre
sin producir lesión celular, de forma que la calidad de la señal se
reduce en pacientes febrile Un abordaje ligeramente diferente
consiste en medir la corriente eléctrica necesaria para mantener
una temperatura constante en la punta del catéter. Éste es el prin-
cipio de un anemómetro de cable caliente a temperatura constante
(que se utiliza para medir el flujo de gas en túneles de aire y en
algunas máquinas de anestesia) aplicado al gasto cardíaco.
La tasa de producción de dióxido de carbono o de consumo
de oxígeno puede utilizarse para medir el gasto cardíaco usando
modificaciones de la ecuación de Fick (v. apéndice 6). Si se emplean
estas variables, un cambio del índice metabólico puede provocar
errores en la medida del gasto cardíaco.
Medidores de flujo por velocidad/presión
(Venturi, Pitot)
Cuando un fluido fluye en un tubo genera velocidad y presión, que
pueden utilizarse de manera indirecta para medir el flujo. La
presión de los fluidos puede considerarse una forma de energía
potencial, como se describió más arriba. La energía cinética en
los fluidos se expresa en términos de flujo, el movimiento general del
fluido con dirección y magnitud determinadas. La energía poten-
cial de la presión puede convertirse en la energía cinética del flujo;
por ejemplo, la presión hidrostática generada por la gravedad que
actúa sobre una columna vertical de líquido puede transformarse
en flujo abriendo una válvula situada en la parte inferior de la
columna. La presión y el flujo también pueden cambiar de forma
independiente. Si se utiliza el sistema circulatorio humano como
ejemplo, un paciente joven y sano con un traumatismo que tiene
shock hipovolémico puede tener la presión arterial normal, pero el
flujo sanguíneo es lento si la resistencia vascular sistémica es
elevada. Un paciente séptico puede tener la presión arterial muy
baja acompañada de flujo sanguíneo alto y resistencia vascular
sistémica baja (shock séptico de alto gasto). La energía mecánica
total de un líquido en movimiento es la suma de la energía cinética
(flujo) y la energía potencial (presión) (v. ).
Un gradiente de presión (presión que cambia en una direc-
ción espacial particular) ejerce una fuerza sobre el fluido, que
tiende a acelerar en la dirección donde hay menos presión. El
gradiente de presión es sólo una de las fuerzas que normalmente
actúan sobre los fluidos; otras fuerzas son la gravedad (que se ha
tratado antes) y la fuerza viscosa o fricción. Si estas otras fuerzas
son despreciables y el fluido no puede comprimirse (p. ej., un fluido
con densidad constante), la ecuación de movimiento (F=ma)
puede integrarse para obtener:
P + ½ρU2 = P0 (7)
donde P es la presión, ρ es la densidad del fluido, U es la magnitud
de la velocidad del fluido y P0 es una constante denominada
«presión de estancamiento» (v. apéndice 5). Esta forma de la ecua-
ción de Bernoulli dice que en un fluido exento de fricción al
aumentar la velocidad, la presión disminuye, y viceversa. Este con-
cepto resuelve la idea errónea común de que la presión siempre se
reduce en la dirección del flujo. En el fluido que hay dentro de un
tubo (una cañería o una vena grande) con un diámetro que crece
gradualmente, la velocidad del fluido (U) disminuye al avanzar
cuando el diámetro y la sección transversal del tubo se incremen-
tan. Cuando U se reduce, la ecuación 7 dice que P aumenta en la
dirección del flujo. Este ejemplo muestra la relación entre la energía
potencial y la energía cinética de los fluidos: como la energía ciné-
tica de este fluido del tubo disminuye (U2 se cae) en la dirección
del flujo, la energía potencial se incrementa (P sube) en la misma
cantidad. La energía total permanece constante porque se ha con-
siderado que no había fricción.
El flujo puede determinarse conociendo la velocidad media
del fluido en el tubo. En el flujo laminar A), el perfil de
velocidades tiene una forma parabólica, de forma que la velocidad
más alta se encuentra en el centro y el fluido de los bordes es casi
estacionario. En el flujo turbulento, el perfil de velocidades es
«plano» como se muestra en la .
La ecuación de Bernoulli se aplica a un subconjunto especí-
fico de flujos sin fricción, que se ha enumerado más arriba. Muchos
984 Control de la anestesia III
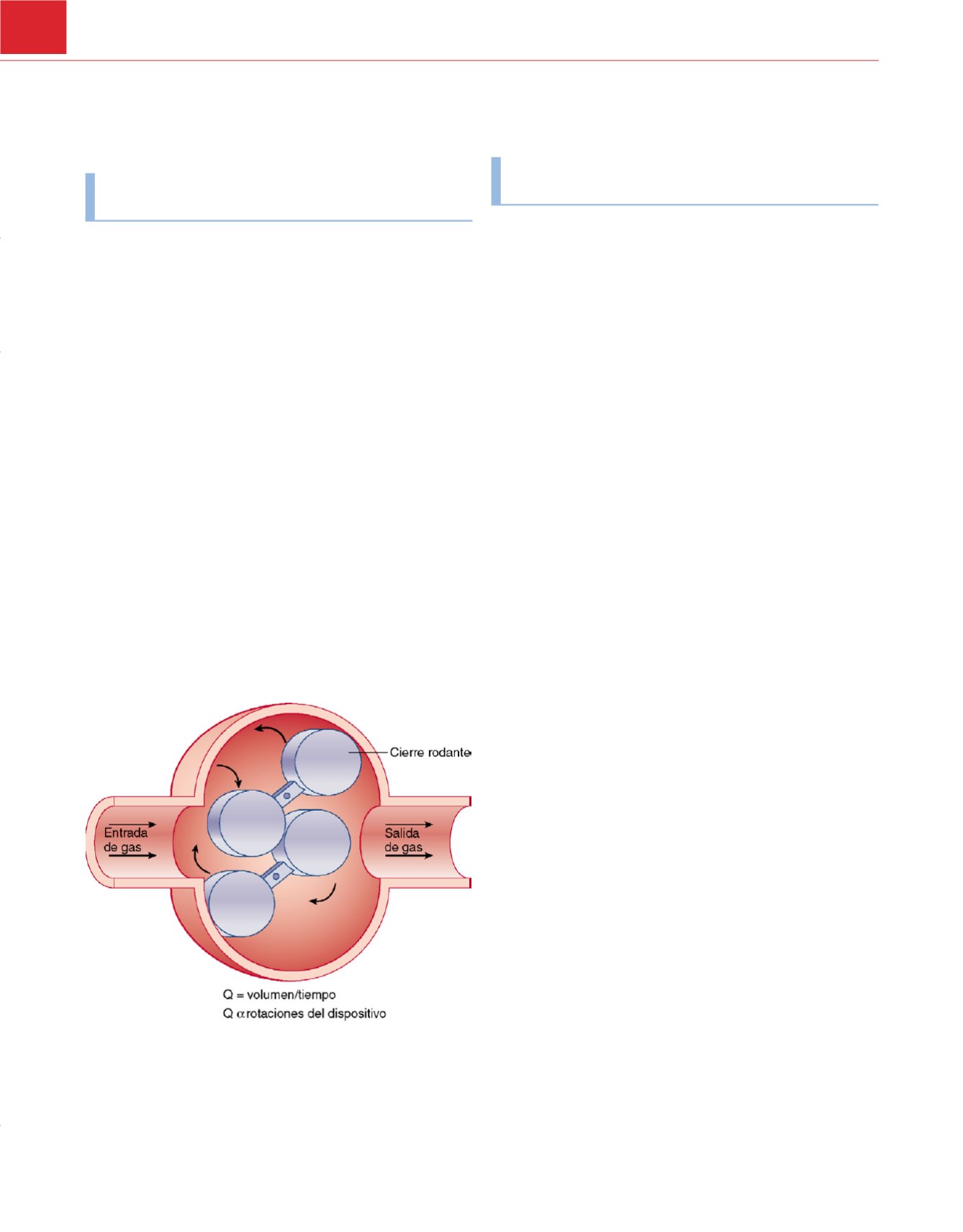
Figura 28-31Volúmetro. El flujo puede describirse como volumen a lo largo
del tiempo. Este diseño para medir el flujo permite al gas pasar sólo en
alícuotas pequeñas, cada una de las cuales se vuelve un contador para medir
la cantidad de flujo. Cuando se divide por el tiempo, este método sirve para
medir el flujo. (Adaptada de Ehrenwerth J, Eisenkraft J: Anesthesia
Equipment: Principles and Application. St. Louis, Mosby-Year Book, 1993.)