
Equilibrio acidobásico perioperatorio
1325
39
Sección III
Control de la anestesia
© ELSEVIER. Fotocopiar sin autorización es un delito
1. Neutralidad eléctrica: en soluciones acuosas, en cualquier
compartimento la suma de todos los iones de carga positiva
debe ser igual a la suma de todos los iones de carga negativa.
2. Equilibrios de disociación: en todo momento se deben satis-
facer los equilibrios de disociación de todas las sustancias
disociadas de forma incompleta, según se deriva de la ley de
acción de masas.
3. Conservación de la masa: la cantidad de una sustancia per-
manece constante salvo que se añada, elimine, genere o des-
truya. La concentración total de una sustancia disociada de
forma incompleta es la suma de las concentraciones de
sus formas disociada y no disociada.
Para determinar el estado acidobásico de un líquido se
deben tener en consideración todas las sustancias a las que se
pudieran aplicar estas reglas. A continuación se presenta una dis-
cusión de los principales grupos.
Ácidos fuertes
Es fácil incorporar el primer grupo de iones, los ácidos fuertes,
porque se disocian por completo. Los iones fuertes más abundantes
en el espacio extracelular son Na
+
y Cl
−
. Otros iones importan
tes incluyen K
+
, SO
4
2−
, Mg
2+
y Ca
2+
. En una solución que contiene áci
dos fuertes creados utilizando concentraciones específicas de NaOH
y de HCl, la concentración de iones de hidrógeno se puede calcu
lar resolviendo la ecuación para que haya neutralidad eléctrica:
([Na
+
] − [Cl
−
]) + ([H
+
] − [OH
−
]) =0
Esto crea dos ecuaciones separadas y simultáneas, como sigue:
[H
+
]=
√
_________________________________
K
w
9
+
(
[Na
+
]−[Cl
−
]
)
2
4 −
(
[Na
+
]−[Cl
−
]
)
2
y
[OH
−
]=
√
__________________________________
K
w
9
+
(
[Na
+
]−[Cl
−
]
)
2
4 −
(
[Na
+
]−[Cl
−
]
)
2
Estas ecuaciones nos dicen que las concentraciones de iones
de hidrógeno e hidroxilo están determinadas por K
W
9
y por la
diferencia de carga entre el sodio y el cloruro. Como la primera es
constante, en este sistema el valor de ([Na
+
] − [Cl
−
]) debe determi-
nar los valores de [H
+
] y [OH
−
]. Como se conocen las concentra-
ciones de sodio y cloruro, se puede cuantificar la carga positiva neta
menos la carga negativa neta. Es la diferencia de iones fuertes
(DIF). Lógicamente, en cualquier solución la suma total de las
cargas de los cationes fuertes menos las cargas de los aniones
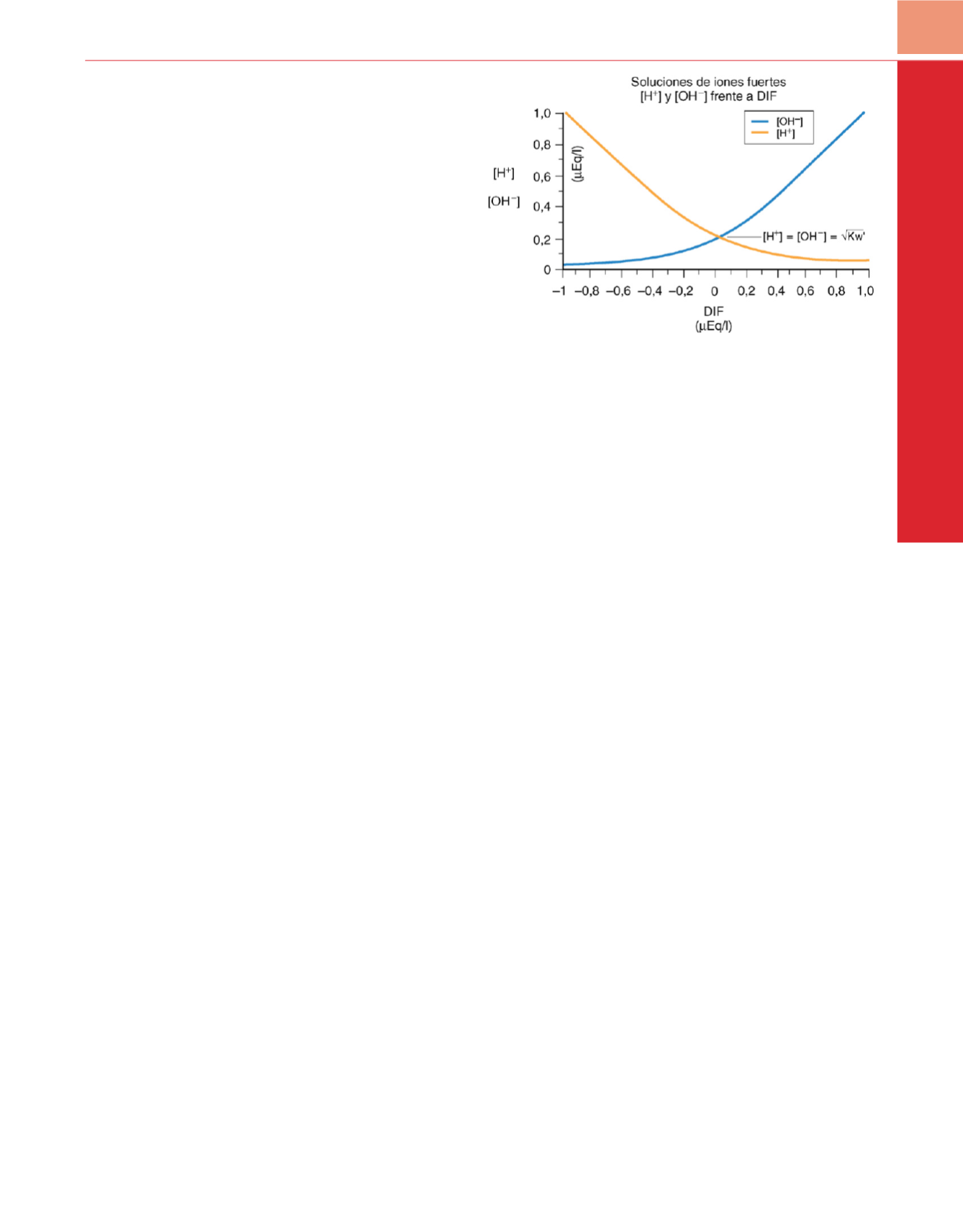
fuertes representa la DIF. La DIF influye de forma independiente
en la concentración de iones de hidrógeno
( fig. 39-1). En el LEC
humano la DIF es positiva:
DIF =
(
[Na
+
]+[K
+
]+[Ca
2+
]+[Mg
2+
]
)
−
(
[Cl
−
]+[A
−
]
)
= 40 a 44 mEq
l
El trabajo pionero de Stewart mostró varios factores en rela-
ción con [H
+
] que no se habían comprendido previamente. La DIF
siempre es positiva en el LEC humano, y los iones de hidroxilo
casi siempre superan cuantitativamente a los iones de hidrógeno
en solución. En estas condiciones la relación entre DIF y [H
+
] no
es lineal. Cualquier cambio de DIF produce modificaciones de las
concentraciones de [H
+
] y [OH
−
]. Debido a la constante de diso-
ciación del agua, esta relación se invierte: cuando aumenta [H
+
],
[OH
−
] disminuye. La DIF es una variable independiente; [H
+
] y
[OH
−
] son dependientes, lo que significa que la adición de iones de
hidrógeno solos (sin los correspondientes aniones fuertes) no
puede influir en el pH de la solución.
Soluciones «amortiguadoras» de ácidos débiles
El grado de disociación del agua (y la concentración de iones de
hidrógeno) también depende de las cargas que generan los ácidos
débiles. Estos ácidos débiles son compuestos disociados parcial-
mente cuyo grado de disociación está determinado por la tempe-
ratura y el pH de la solución. Las moléculas predominantes en este
grupo son albúmina y fosfato. Stewart utilizó el término A
TOT
para
representar la concentración total de iones débiles que influían en
el equilibrio acidobásico
10 .El ácido HA se disocia tan sólo parcialmente, lo que está
representado por el siguiente equilibrio:
[HA] = K
A
[H
+
] [A
−
]
K
A
es la constante de disociación del ácido débil. Si asumi-
mos que HA y A
−
no tienen ninguna otra participación en esta
reacción (la ley de la conservación de la masa), la cantidad de A
−
presente en la solución debe ser igual a la cantidad presente ini-
cialmente, por lo que:
[HA][A
−
] = [A
TOT
]
donde [A
TOT
] es la concentración total de ácidos débiles.
Para calcular el efecto de la disociación de los ácidos débiles
sobre [H
+
] debemos tener en consideración la disociación del agua
y la neutralidad eléctrica:
[H
+
] [OH
−
] = K
w
9
(disociación del agua)
[DIF]+[H
+
]−[A
−
]−[OH
−
] = 0 (neutralidad eléctrica)
Estas cuatro ecuaciones simultáneas determinan el valor de
[H
+
] de esta solución que contiene iones fuertes y ácidos débiles. DIF
yA
TOT
son variables independientes cuya concentración se determinó
durante la producción del sistema. K
W
9
y K
A
son constantes. En con-
secuencia, las otras variables [HA], [H
+
], [OH
−
] y [A
−
] se deben
ajustar para satisfacer las ecuaciones. Son variables dependientes.
Dióxido de carbono
Junto a los iones fuertes y las bases débiles, el LEC contiene CO
2
.
La concentración de CO
2
en el LEC está determinada por su pro-
ducción en los tejidos y por la ventilación alveolar. Cuando está en
solución, el CO
2
aparece en cuatro formas: CO
2
[denominado
CO
2
(d)], ácido carbónico (H
2
CO
3
), iones de bicarbonato (HCO
3
−
)
y iones de carbonato (CO
3
2−
).
Figura 39-1
Efecto de los cambios del hiato de iones fuertes (diferencia de
iones fuertes [DIF]) sobre las concentraciones de los iones de hidrógeno e
hidroxilo.
(Adaptado de Stewart PA: Modern quantitative acid-based
chemistry.
Can J Physiol Pharmacol
61:1444-1461, 1983.)









