
dosis conocida de un fármaco y midiendo las concentraciones plas-
máticas resultantes. El modelo matemático relaciona la entrada del
fármaco a lo largo del tiempo, I(t), con la concentración a lo largo
del tiempo, C(t). Estos modelos pueden adoptar múltiples formas.
La
figura 18-4representa la concentración plasmática a lo largo del
tiempo después de un único bolo intravenoso de un fármaco en el
momento 0. Las concentraciones del fármaco disminuyen de forma
continua después de administrar el bolo, y la velocidad de dismi-
nución es aproximadamente proporcional a la cantidad de fármaco
que hay en el plasma. Es conveniente describir este comportamiento
mediante modelos exponenciales. La curva puede tener un único
exponente; en este caso, la concentración plasmática a lo largo del
tiempo se puede describir con la función C(t) =Ae
–kt
, donde A es la
concentración en el momento 0 y k una constante que describe
la velocidad a la que la concentración se reduce. La relación parece
ser una línea recta cuando se representa como el logaritmo de la
concentración frente al tiempo. La farmacocinética de los fármacos
anestésicos intravenosos es más compleja porque, después del bolo,
se observa un período de disminución rápida antes de la parte del
«logaritmo lineal» (es decir, la parte que es una línea recta cuando
se representa como logaritmo de la concentración frente al tiempo).
Podemos hacer un modelo de esta relación tomando varias curvas
monoexponenciales (es decir, con un exponente) y colocándolas
juntas. De esta manera se consigue una curva poliexponencial. Por
594
Farmacología y anestesia
II
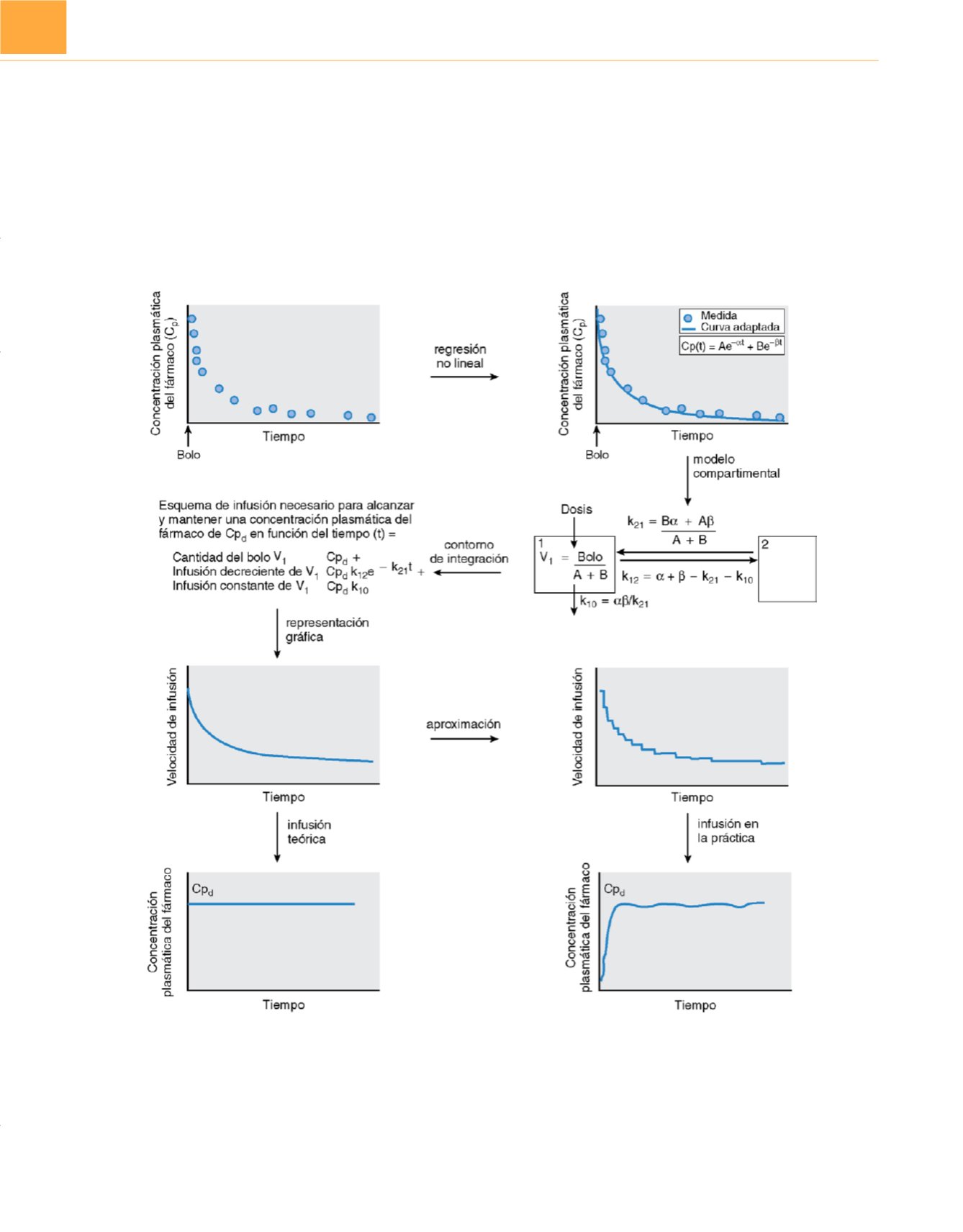
Figura 18-4
Pasos que están implicados en un algoritmo farmacocinético de infusión. Normalmente, los algoritmos farmacocinéticos derivan de experimentos
en los que la concentración plasmática del fármaco se mide a intervalos tras la administración de un bolo del fármaco. Se utiliza la regresión no lineal para
adaptar a una curva monoexponencial, biexponencial o triexponencial los datos obtenidos de la concentración frente al tiempo. Existe una relación algebraica
entre las curvas de disminución exponencial y los modelos farmacocinéticos de uno, dos y tres compartimentos. Se desarrolla el esquema de infusión «BET»,
que se compone de un bolo, una infusión continua que sustituye al fármaco eliminado del cuerpo y una infusión que disminuye exponencialmente para
reemplazar al fármaco que se traspasa del plasma a otros compartimentos del cuerpo. La infusión BET consigue mantener una determinada concentración
plasmática constante. La implantación práctica del esquema BET con bombas de infusión reales y velocidades de infusión que sólo cambian en determinados
intervalos logra un perfil de concentración plasmática del fármaco que se aproxima al perfil que resulta de una infusión BET.









