
0,5. De aquí procede el término «C
50
»: es la concentración asociada
a una respuesta del 50%. Conforme C se hace mucho mayor que
C
50
, la ecuación se aproxima a
C
__
C
, que es 1. La
figura 9-5muestra la
forma de esta relación, que es lineal a concentraciones bajas, pero
a concentraciones altas la respuesta se satura a 1.
Podemos crear un modelo para la relación entre metabo-
lismo hepático y concentración de fármaco con esta ecuación de
saturación, pero ¿qué concentración determina la tasa de metabo-
lismo?: ¿la concentración de entrada en el hígado, la concentración
media en el interior del hígado o la concentración de salida del
hígado? Se han utilizado las tres, pero el modelo más empleado
considera que la tasa de metabolismo es una función de la concen-
tración de
salida
del hígado, C
salida
. Este aspecto ha sido estudiado
con detalle por Wagne
r 3.
Podemos ampliar la ecuación de metabolismo para incluir la
observación de que la tasa de metabolismo, R, se aproxima a la satu-
ración con la tasa metabólica máxima, V
m
, como función de C
salida
:
Tasa de metabolismo del fármaco = R = Q˙
(
C
entrada
− C
salida
)
= V
m
C
salida
_________
K
m
+ C
salida
(4)
V
m
es la tasa metabólica máxima posible. La parte de saturación de
esta ecuación,
C
salida
_______
K
m
+C
salida
, determina la fracción de la tasa metabólica
máxima. K
m
, denominada también constante de Michaelis, es la
concentración de salida correspondiente a una tasa metabólica
del 50% de V
m
. La
figura 9-6muestra gráficamente esta relación.
El eje
x
es la concentración de salida, C
salida
, como fracción de
V
m
, la concentración que produce el 50% de la tasa metabólica
máxima. El eje
y
es la tasa de metabolismo del fármaco como
fracción de V
m
, la tasa máxima de metabolismo del fármaco. Al
normalizar C
salida
para K
m
y la tasa metabólica para V
m
, la rela-
ción de la
figura 9-6es cierta para todos los valores de V
m
y K
m
.
La
figura 9-6muestra que, mientras la concentración de salida
sea menor que la mitad de K
m
, existe un cambio casi proporcio-
nal en la tasa metabólica, con un cambio proporcional en la
concentración de salida. En la mayoría de los anestésicos, las concentraciones clínicas no superan la mitad de K
m
por lo que su
metabolismo es casi proporcional a la concentración. También
podemos interpretar la
figura 9-6respecto a la tasa metabólica
(eje
y
). Mientras la tasa metabólica sea menor de un tercio de
la capacidad metabólica máxima, la tasa de metabolismo
aumenta proporcionalmente a la concentración. El mensaje
clínico es que el metabolismo es proporcional a la concentra-
ción y por tanto la farmacocinética se mantiene lineal siempre
que la velocidad de administración intravenosa en equilibrio no
supere un tercio de la capacidad metabólica máxima.
Principios básicos de farmacología
249
9
Sección II
Farmacología y anestesia
© ELSEVIER. Fotocopiar sin autorización es un delito
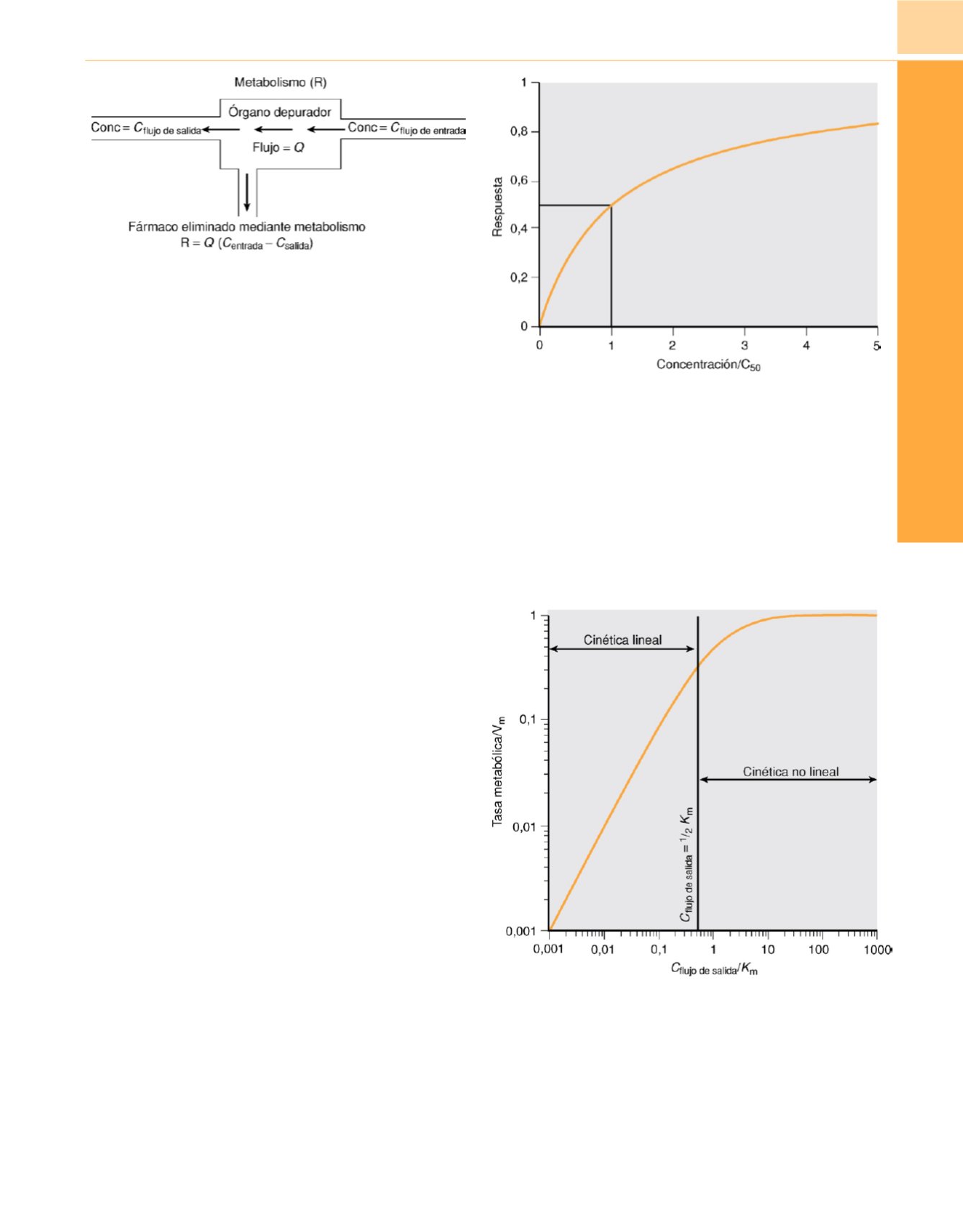
Figura 9-4
La tasa de metabolismo puede computarse como la velocidad del
flujo sanguíneo hepático por la diferencia entre la concentración del fármaco
en el flujo de entrada y de salida. Se trata de un método frecuente para
analizar el metabolismo o la captación tisular en un órgano en estudios
farmacocinéticos de equilibrio de masa.
Figura 9-5
Ecuación de saturación, respuesta = C/(C
50
+C), que muestra la
disminución del aumento de respuesta conforme el sistema se aproxima a
la saturación. En farmacocinética y farmacodinámica se emplean variantes
de esta ecuación.
Figura 9-6
Relación entre concentración, expresada como fracción de K
m
(constante de Michaelis) y metabolismo del fármaco, expresado como
fracción de V
m
(velocidad máxima). Mientras la concentración de salida sea
menor que la mitad de K
m
, un cambio en la concentración se acompaña de
un cambio proporcional en la tasa metabólica. Esto es cierto para casi todos
los fármacos anestésicos. (
Modificado de Shafer S: Principles of
pharmacokinetics and pharmacodinamics
. En
Longnecker DE, Tinker JH,
Morgan GE [eds.]:
Principles and Practice of Anesthesiology,
2.
a
ed. St. Louis,
Mosby-Year Book, 1997.
)









