
ln(x
1
) − ln x
1
__
2
= ln
(
x
1
__
x
1
__
2
)
= ln(2)
≈ 0,693
(24)
Esto relaciona de modo sucinto la pendiente (o «constante de velo-
cidad»), k, con la semivida, t
1/2
:
k = 0,693 _____
t
1/2
(25)
Por tanto, si medimos el tiempo que tarda x en bajar al 50%, t
1/2
,
conocemos la constante de velocidad k. Si conocemos k, podemos
deducir fácilmente de la ecuación 25 el tiempo que tarda x en bajar
al 50%:
t
1/2
= 0,693 _____
k
(26)
Modelos farmacocinéticos fisiológicos
Es posible analizar volúmenes y depuraciones para cada órgano
del cuerpo y construir modelos de farmacocinética ensam-
blando los modelos de estos órganos en modelos anatómica y
fisiológicamente precisos de todo el animal. La
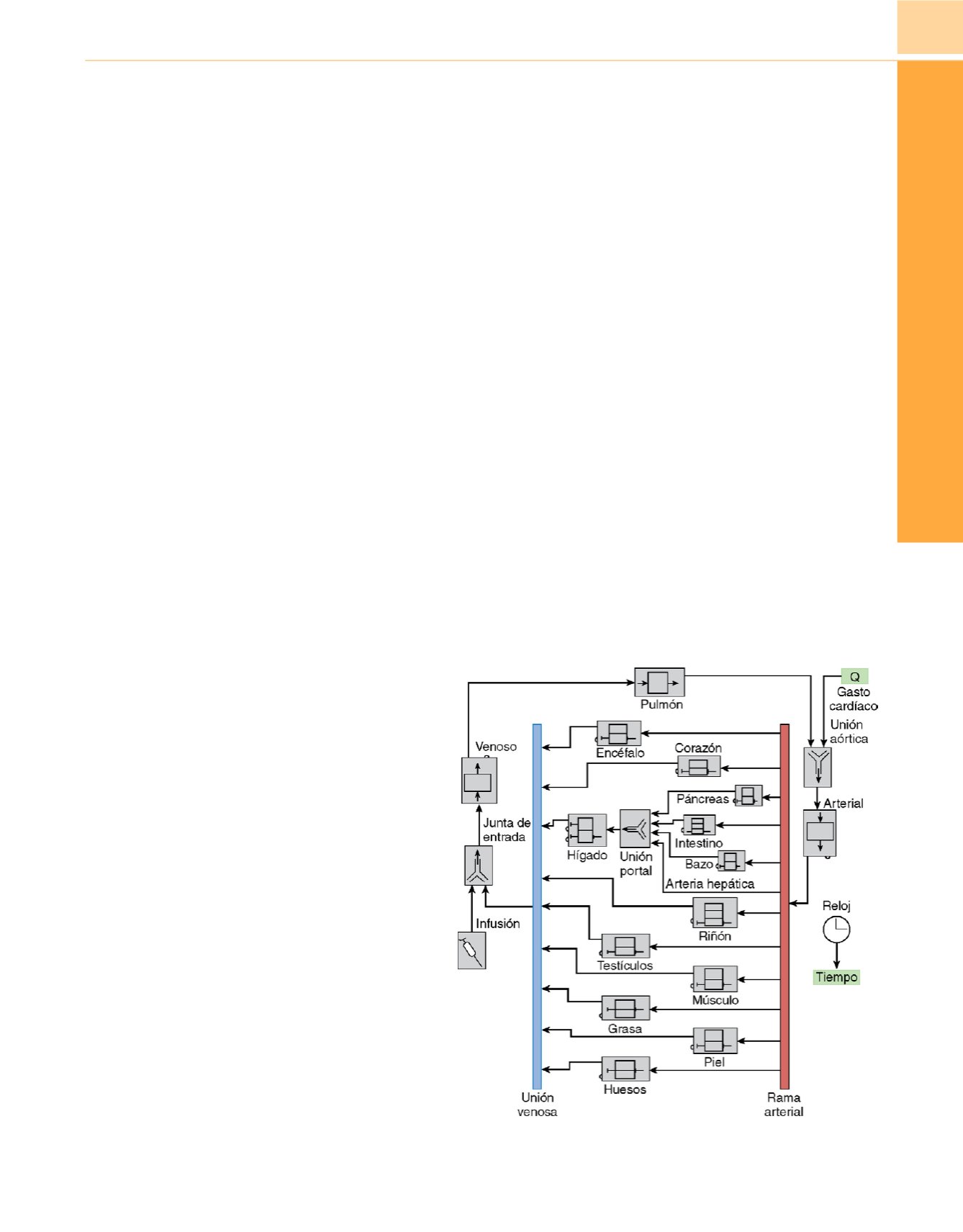
figura 9-14muestra este modelo para el tiopental en la rat
a 6. Estudios pos-
teriores han demostrado que estos modelos de volúmenes tisu-
lares y flujos sanguíneos individuales pueden trasladarse de la
rata al ser humano para obtener modelos precisos de farmaco-
cinética en el ser human
o 7. Esto demuestra la utilidad potencial
de los modelos farmacocinéticos basados en la fisiología para
elaborar modelos farmacocinéticos humanos a partir de modelos
animales.
Los modelos válidos para tejidos individuales son mate-
máticamente complicados y no predicen mejor la concentración
plasmática del fármaco que los modelos que agrupan los tejidos
en varios compartimentos. Si el objetivo es determinar cómo
administrar ciertos fármacos para obtener concentraciones plas-
máticas terapéuticas, todo lo necesario es relacionar matemáti-
camente la dosis con la concentración plasmática. Para este
propósito suelen ser adecuados los modelos «compartimenta-
les» convencionales.
Modelos farmacocinéticos compartimentales
Estos modelos se sustentan en los mismos conceptos básicos que
los modelos fisiológicos aunque con simplificaciones más burdas.
El «modelo unicompartimental» de la
figura 9-15contiene un
volumen único y una depuración única, como si el ser humano
estuviera hecho como cubos. Para los fármacos anestésicos, utili-
zamos el símil de varios cubos conectados por tuberías. Esto suele
representarse con modelos bi o tricompartimentales también pre-
sentes en la
figura 9-15. El volumen de la derecha en el modelo
bicompartimental, y el del centro en el modelo tricompartimental,
es el volumen central. Los restantes son los volúmenes periféricos.
La suma de todos los volúmenes es el volumen de distribución en
equilibrio, Vd
ee
. La depuración del compartimento central es la
depuración «central» o «metabólica». Las depuraciones entre el
compartimento central y los compartimentos periféricos son las
depuraciones «intercompartimentales».
Principios básicos de farmacología
255
9
Sección II
Farmacología y anestesia
© ELSEVIER. Fotocopiar sin autorización es un delito
Figura 9-14
Modelo fisiológico del tiopental en ratas. La
farmacocinética de distribución en cada órgano se determina de modo
individual. Los componentes del modelo están conectados por
procesos de orden cero (flujo) y primer orden (difusión). (
De Ebling WF,
Wada DR, Stanski DR: From piecewise to full physiologic
pharmacokinetic modeling: Applied to thiopental disposition in the rat.
J Pharmacokinet Biopharm
22:259-292, 1994.
)









