
observada en la
figura 9-13. Podemos calcular la depuración, D, de
dos maneras. Primero, podemos calcular V reordenando la defini-
ción de concentración, V=dosis/concentración inicial =dosis/C
0
.
Volviendo a la ecuación 28, si medimos la pendiente, –k, podemos
calcular la depuración como k × V. Una solución más general es
considerar la integral de la curva de concentración en el tiempo,
ecuación 30, conocida en farmacocinética como área bajo la curva
(ABC):
Podemos reordenar la ecuación 31 para despejar la depuración, D:
D = x
0
_____
ABC
(32)
Como x
0
es la dosis de fármaco, la depuración se iguala a la dosis
dividida por el ABC. Esta propiedad fundamental de los modelos
farmacocinéticos
lineales
se aplica a los modelos unicompartimen-
tales, multicompartimentales y a cualquier tipo de dosificación de
fármaco intravenoso (siempre que la dosis
total
administrada por
vía sistémica sea el numerador). Como consecuencia directa, el
ABC es proporcional a la dosis en los modelos lineales (es decir,
modelos en los que D es constante).
F
armacocinética
de
infusión
.
Cuando se administra
una infusión a una velocidad E (entrada), la concentración plas-
mática aumenta mientras la velocidad de entrada de fármaco en el
organismo, E, supere la velocidad de salida del mismo, C×D, donde
C es la concentración de fármaco. Cuando E=C×D, el fármaco
entra y sale con la misma velocidad, y el organismo está en equili-
brio. Podemos calcular la concentración en equilibrio observando
que la velocidad de entrada de fármaco debe ser igual a la velocidad
de salida del fármaco. A partir de la ecuación 6 sabemos que la
velocidad de metabolización del fármaco en equilibrio es
Tasa metabólica=C
ee
×D
(33)
donde C
ee
es la concentración arterial en equilibrio. Dado que por
definición, la velocidad de infusión en equilibrio debe igualar la
tasa metabólica, y la velocidad de infusión, E, en equilibrio debe
ser E=C
ee
×D. Resolviendo la ecuación para la concentración en
equilibrio, C
ee
, da
E
__
D
. Por tanto, la concentración en equilibrio
durante una infusión es la velocidad de entrada del fármaco dividida
por la depuración. Se deduce que para calcular la velocidad de infu-
sión que permite conseguir una concentración deseada, C
D
, en equi-
librio, la velocidad de infusión debe ser C
D
×D.
Principios básicos de farmacología
257
9
Sección II
Farmacología y anestesia
© ELSEVIER. Fotocopiar sin autorización es un delito
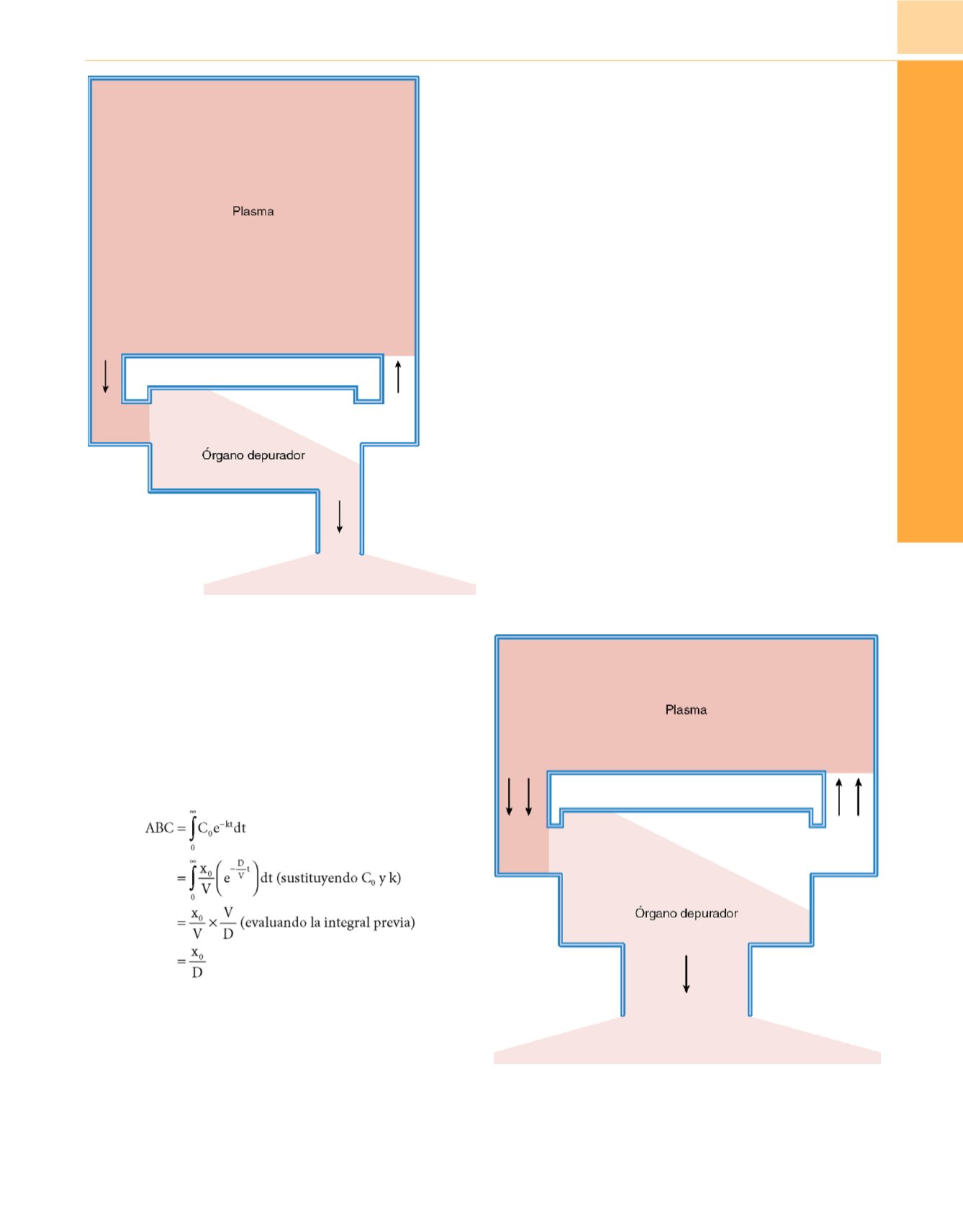
Figura 9-16
Modelo unicompartimental similar al de la
figura 9-3pero con más
volumen de distribución. Tras la administración del fármaco, las concentraciones
descienden más lentamente en este modelo que en el de la
figura 9-3 .Figura 9-17
Modelo unicompartimental similar al de la
figura 9-3pero con
más depuración. Tras la administración del fármaco las concentraciones
descienden con más rapidez en este modelo que en el de la
figura 9-3 .(31)









