
Modelo unicompartimental
F
armacocinética
del
bolo
.
Piense en el cuerpo como
un cubo en el que vertemos un fármaco. La cantidad de
fármaco vertido en el cubo es x
0
(x en el tiempo 0). La con-
centración inicial es x
0
/V, donde V es el volumen de líquido en
el cubo. Volviendo a la ecuación 1, si conocemos la concentra-
ción que queremos conseguir, la concentración deseada, C
D
, y
el volumen en el cubo, V, podemos calcular la dosis para con-
seguir C
D
reordenando la definición de concentración:
Dosis = C
D
×V.
Podemos suponer que el líquido está atravesando un
órgano de depuración con una velocidad constante que denomi-
namos depuración, D. ¿Cuál es la velocidad, dx/dt, con la que el
fármaco sale del cubo? Como la concentración es x/V y D es la
velocidad de salida del líquido del cubo a través del órgano
depurador, la velocidad con la que el fármaco sale del cubo debe
ser x/V x D. Esta velocidad es un proceso de primer orden si, y
sólo si, es igual a una constante,
k
, por la cantidad de fármaco en
el cubo. ¿Es así?
dx ___
dt
= x __
V
D
(27)
= D __
V
x
= kx?
Establecimos antes que el flujo a través del órgano depurador,
D, es constante. El volumen, V, es constante porque el órgano
depurador devuelve el flujo al cubo. Dado que D y V son constan-
tes,
D
__
V
es también una constante. Volviendo a la
ecuación 27 ,k, por
definición una constante de procesos de primer orden, se iguala
a
D
__
V
, por definición una constante de depuración y volumen.
Podemos reordenarla para obtener la identidad fundamental de la
farmacocinética lineal:
D(depuración) = k (constante de velocidad)
× V (volumende distribución)
(28)
¿Qué revela esta fórmula sobre las relaciones entre semivida,
volumen y depuración? Reordenando la ecuación previa como
k=
D
__
V
y recordando que t
1/2
=
0,693
____
k
, podemos concluir que la semi-
vida es proporcional al volumen e inversamente proporcional a la
depuración:
t
1/2
= 0,693 V __
D
t
1/2
∝
V __
D
(29)
La
figura 9-16muestra un modelo unicompartimental con una
depuración idéntica pero con un volumen mayor que el de la
figura 9-3 .Como predice la ecuación previa, la semivida aumenta porque
tarda más en eliminarse el fármaco de este mayor volumen. La
figura 9-17muestra un modelo unicompartimental con un volumen idén-
tico pero una depuración más rápida que en la
figura 9-3 .Las concen-
traciones descienden más deprisa (es decir, semivida más corta) con
mayor depuración, como predice la ecuación 29.
Como se trata de un proceso de primer orden,
dx
__
dt
=kx, y la
integral indica la cantidad de fármaco en el tiempo t en términos
de cantidad en el tiempo 0, x(t) =x
0
e
−kt
, si dividimos ambos lados
por V y recordamos que x/V es la definición de la concentración,
obtenemos la ecuación que relaciona la concentración tras un bolo
intravenoso con el tiempo y la concentración inicial:
C(t)=C
0
e
−kt
(30)
Esta ecuación define la curva «concentración en el tiempo» para
un modelo unicompartimental, y tiene la forma lineal-logarítmica
256
Farmacología y anestesia
II
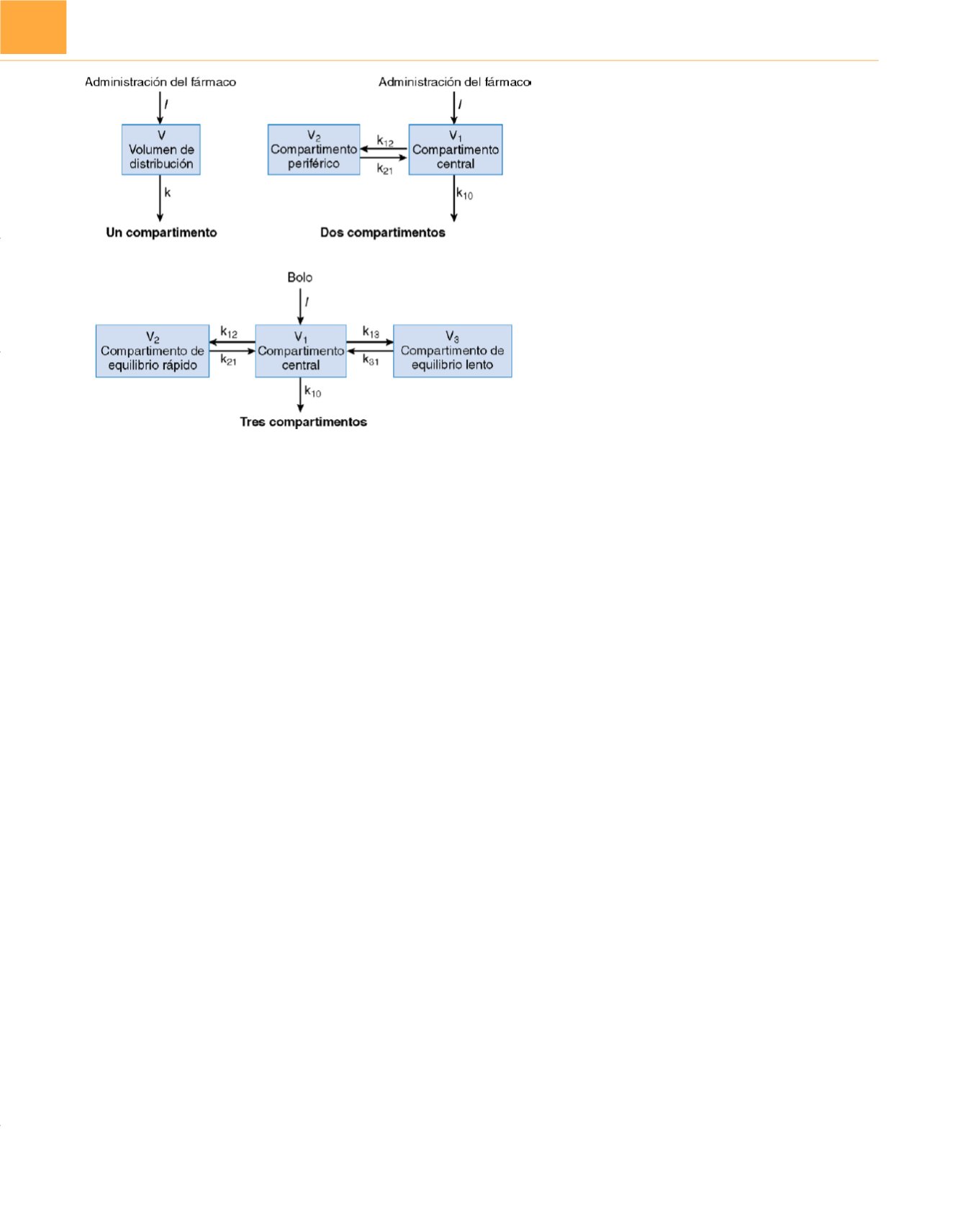
Figura 9-15
Modelos mamilares uni, bi y tricompartimentales.
f0080









