
los enantiómeros de bupivacaína y ketamina, y el levoisómero de la
bupivacaína se comercializa como levobupivacaína. Aunque existe
una apreciación generalizada de la importancia del estudio de la far-
macocinética y farmacodinámica de estereoisómeros individuales, la
dificultad de estos estudios ha impedido su generalización.
Modelos farmacocinéticos
Procesos de orden cero y de primer orden
El consumo de oxígeno y la producción de dióxido de carbono por
el organismo son procesos con una velocidad constante y se deno-
minan procesos de orden cero. La velocidad de cambio (dx/dt) de
un proceso de orden cero es
dx ___
dt
= k
(17)
La ecuación 17 establece que la velocidad de cambio es constante.
Si x representa una cantidad de fármaco y t representa el tiempo,
las unidades de k son cantidad/tiempo. Para hallar el valor de x en
el tiempo t, x(t), podemos calcularlo como la integral para la ecua-
ción 17 de tiempo 0 a tiempo t:
x(t) = x
0
+ k × t
(18)
donde x
0
es el valor de x en el tiempo 0. Se trata de la ecuación de
una línea recta con una pendiente k y una intersección de x
0
.
Numerosos procesos suceden a una velocidad proporcional
a la cantidad. Por ejemplo, el pago de intereses de un préstamo es
proporcional al balance pendiente, y la velocidad a la que drena el
agua de una bañera es proporcional a la cantidad (altura) de agua
en la bañera. Estos son ejemplos de procesos de primer orden. La
velocidad de cambio en los procesos de primer orden es sólo lige-
ramente más compleja que en los procesos de orden cero:
dx ___
dt
= k × x
(19)
La unidad k es 1/tiempo porque x en el lado derecho ya incluye las
unidades de cantidad. El valor de x en el tiempo t, x(t), puede
calcularse como la integral desde el tiempo 0 al tiempo t:
x(t) = x
0
× e
kt
(20)
donde x
0
es el valor de x en el tiempo 0. Si k es mayor de cero, x(t)
aumenta de modo exponencial. Si k es menor de 0, x(t) disminuye
de modo exponencial. En farmacocinética k es negativa porque las
concentraciones disminuyen con el tiempo. Por motivos de clari-
dad el signo menos suele ser explícito, por lo que k se expresa como
número positivo. Por tanto, la ecuación idéntica para la farmaco-
cinética con el signo menos explícito es
x(t) = x
0
× e
−kt
(21)
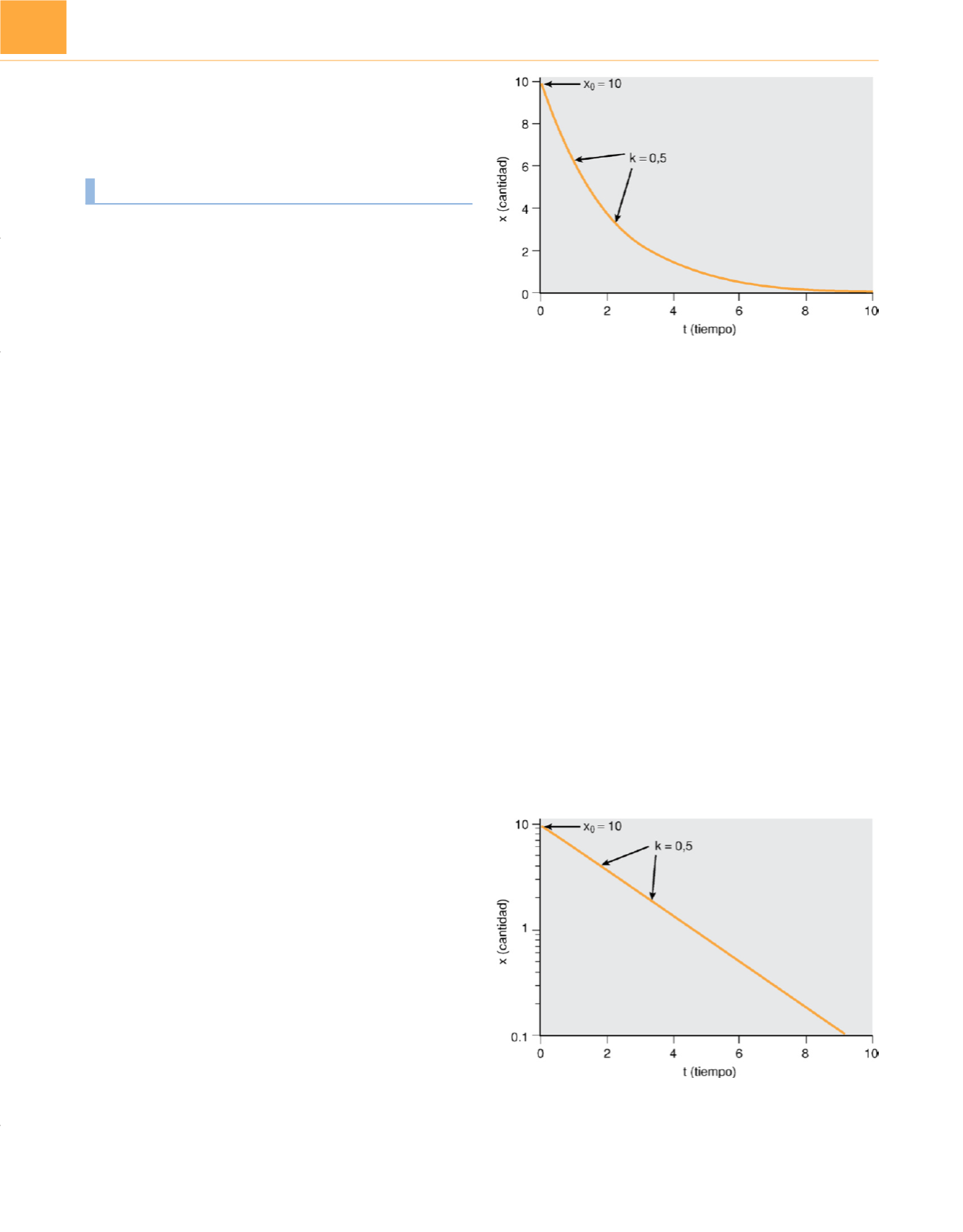
La
figura 9-12muestra la relación entre x y el tiempo como se
describe en la ecuación 21. En la
figura 9-12 ,x disminuye conti-
nuamente con el tiempo aunque la pendiente de la curva asciende
continuamente (es decir, se hace menos negativa). Tomando el
logaritmo natural de ambos lados de la ecuación 21 obtenemos
ln
(
x[t]
)
= ln
(
x
0
× e
−kt
)
= ln
(
x
0
)
+ ln
(
e
−kt
)
= ln
(
x
0
)
−
(
k × t
)
(22)
Es la ecuación de una línea recta como se ve en la
figura 9-13 ,donde el eje vertical es ln(x[t]), el eje horizontal es
t
, la intersección
es ln(x
0
) y la pendiente de la línea es −
k
.
¿Cuánto tarda x desde cierto valor, x
1
, a la mitad de dicho
valor, x
1
/2? Como k es la pendiente de una línea recta que relaciona
ln(x) con el tiempo,
k =
∆
ln(x)
______
∆
t
=
ln(x
1
) − ln
(
x
1
__
2
)
____________
t
1/2
(23)
donde t
1/2
es la «semivida», o el tiempo necesario para un descenso
de
x
a la mitad. Podemos simplificar el numerador
254
Farmacología y anestesia
II
Figura 9-12
Curva de descomposición exponencial, según x(t)=x
0
e
-kt
,
trazada con ejes convencionales, con
x
0
=10 y
k
=0,5.
Figura 9-13
La misma curva de descomposición exponencial, x(t)=x
0
e
-kt
, que
en la
figura 9-12 ,trazada sobre un eje
y
logarítmico.









