Miller Anestesia

611 / 2894

tanto, la fiabilidad de cualquier modelo de sistema de control
depende de lo bien que el modelo represente el proceso que estamos
controlando. En un sistema de asa abierta, el clínico va aprendiendo
acerca del comportamiento del paciente y adapta la administración
del fármaco a las necesidades individuales del paciente.
En un sistema de infusión de asa cerrada con control «adapta-
tivo», es el propio sistema el que mide el efecto del fármaco y ajusta el
modelo interno para representar de una mejor forma al paciente con-
creto. Las señales de asa cerrada requieren mediciones precisas de los
objetivos. Por ejemplo, un sistema de asa cerrada de control de la
presión arterial con nitroprusiato sódico tendrá un esquema de dosi-
ficación esperado que probablemente será bastante conservador para
evitar que se produzca una hipotensión profunda.Conforme el sistema
va aprendiendo la sensibilidad individual del paciente, ajustará la dosi-
ficación del nitroprusiato sódico a la sensibilidad de dicho paciente,
adaptando el modelo farmacocinético/farmacodinámico interno para
que pueda alcanzar de lamejor manera el objetivo clínico.En anestesia,
los sistemas de asa cerrada han utilizado normalmente alguna señal
derivada del EEG como base del control de asa cerrada adaptativo.
Sistemas de infusión mediante control
de concentraciones finales
Sistemas
Kruger-Thieme describió, en 1968, el régimen de infusión nece-
sario para, en teoría, alcanzar pronto y mantener una concentración
plasmática constante de un fármaco administrado por vía intrave-
nosa, cuya cinética se ajustaba a un modelo bicompartimental. Este
régimen se conoce como el «esquema BET» (v. ) y consiste
en un bolo inicial de CTV 1, una infusión a una velocidad de CTCl S
para reemplazar el fármaco eliminado del cuerpo, y una infusión
exponencialmente decreciente a una velocidad determinada por la
ecuación 14 para reemplazar el fármaco que se transfiere a los tejidos
periféricos. En la sección sobre diseño de regímenes de dosis que se
ha visto en párrafos anteriores se demostró que la porción del bolo,
calculada como CTV1, quizá no sea adecuada para alcanzar la con-
centración deseada en el sitio de efecto. Desde el punto de vista
matemático, la porción «ET» del esquema BET es idéntica a la velo-
cidad de infusión de mantenimiento exponencialmente decreciente
que se ha visto en la citada sección «Diseño de regímenes de dosis».
La administración precisa de estos complejos regímenes de dosis
necesita que la velocidad de infusión cambie continuamente a lo
largo del tiempo, hasta que se alcanza el equilibrio estacionario.
Más de una década después de la publicación del ya clásico
artículo de Kruger-Thiemer, Schwilden y cols conectaron un
microprocesador a una bomba de infusión y demostraron la apli-
cación clínica del esquema de infusión BET. Desde entonces,
muchos grupos han implantado el algoritmo BET o modificaciones
del mismo a microprocesadores conectados a bombas de infusión.
Dichos algoritmos se basan en la misma ecuación poliexponencial
o modelo compartimental antes descrito, y calculan la velocidad de
infusión que en teoría es necesaria para conseguir la concentración
plasmática deseada o de fármaco en el sitio de efecto. Cuando se
utilizan estos algoritmos, hay que tener en cuenta las limitaciones
físicas del sistema. Por ejemplo, la velocidad de infusión tiene que
ser positiva o cero. Además, algunas bombas tienen una precisión
y una seguridad limitadas que reducen la precisión de la infusión.
A pesar de las pequeñas modificaciones que han utilizado
diferentes investigadores en el uso de los sistemas de infusión con-
trolados por algoritmos farmacocinéticos, todos ellos son similares
desde una perspectiva conceptual. Todos están formados por un
microprocesador conectado a una bomba de infusión, como se
muestra en la El microprocesador ejecuta un pro-
grama que incorpora el modelo farmacocinético. Cuando utiliza el
dispositivo, el anestesiólogo introduce una concentración plasmá-
tica deseada, o de fármaco en el sitio de efecto ). Esta
concentración objetivo se basa en el conocimiento de la relación
Sistemas de administración de fármacos intravenosos 611 18
Sección II
Farmacología y anestesia
© ELSEVIER. Fotocopiar sin autorización es un delito
Tabla 18-6Esquemas de infusión manua
Anestesia Sedación o analgesia
Fármaco Dosis de carga (mg/kg) Infusión de mantenimiento (m g/kg/min) Dosis de carga (mg/kg) Infusión de mantenimiento (m g/kg/min)
Alfentanilo 50-150 0,5-3 10-25 0,25-1
Fentanilo 5-15 0,03-0,1 1-3 0,01-0,03
Sufentanilo 0,5-5 0,01-0,05 0,1-0,5 0,005-0,01
Remifentanilo 0,5-1,0 0,1-0,4 0,025-0,1
Ketamina 1.500-2.500 25-75 500-1.000 10-20
Propofol 1.000-2.000 50-150 250-1.000 10-50
Midazolam 50-150 0,25-1,5 25-100 0,25-1
Metohexital 1.500-2.500 50-150 250-1.000 10-50
Dexmedetomidina ‡ 0,5-1 en 10 min 0,2-0,7
* Después de la dosis de carga, se debe utilizar una velocidad de infusión más rápida para compensar la redistribución y después ajustarla a la velocidad de infusión más
lenta, que mantendrá la anestesia o la sedación adecuadas. Cuando se utilizan opioides como parte de una técnica de anestesia nitroso-opioides para cirugía cardíaca, se
utiliza el esquema de dosificación que aparece en el listado de anestesia. Cuando se combina el opioide como parte de una anestesia balanceada, es necesaria la dosifica-
ción que aparece en el listado de analgesia.
† Para la analgesia o durante la sedación, no se debe administrar una dosis inicial de carga de remifentanilo debido a que su rápido inicio de acción puede producir apnea
o rigidez muscular.
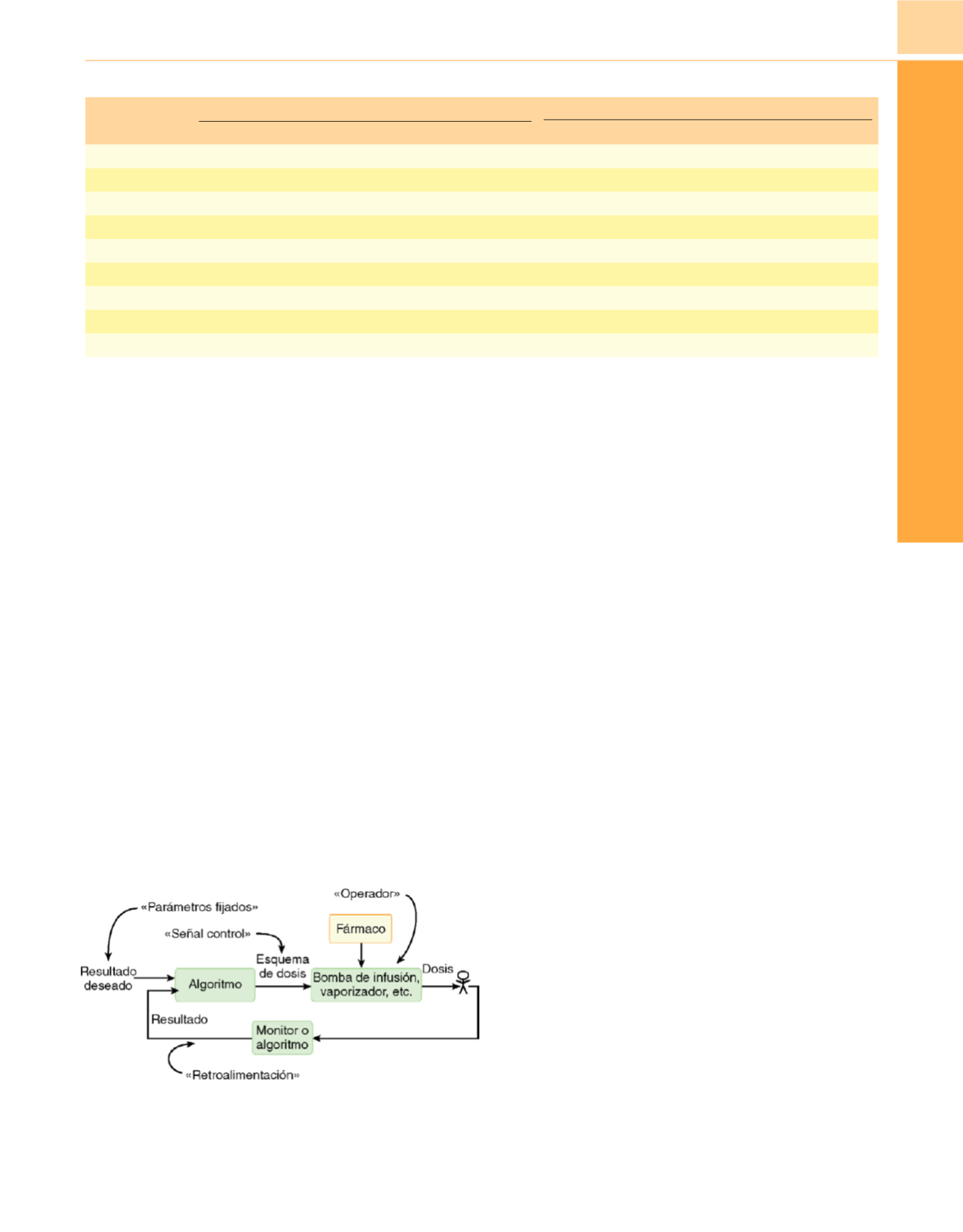
Figura 18-22Componentes de un sistema de administración automática de
fármacos típico.